Home Archives
Contact me		 Guestbook Forbidding chains
for absolute beginners

Andrei's notation

Hi, happy new year and best wishes to everyone ! You are in my sudoku sandbox where I put some proofs of puzzles from sudoku.com.au... As wages for all the typing (and grey cells torturing) it involved, I'd gladly read a little word from you in the Guestbook.

New ! Big thanks to Gath who offers us a splendid site, and whose democratic attitude as a webmaster is a model. He kindly heard and answered the request for new material in tough section. All of us crazy solvers appreciate to have new problems to face and solve !

Proof of

09-12
(19->28 type)		 09-20
(21->27 type)		 09-24
(20->23 type)		 09-28
(21->26 type)		 09-30
(19->51 type)		 01-28 01-29 02-01 New! 02-02 New! 02-03 New! 02-04 New! 02-05
New! 02-06 New! 02-07 New! 02-08 New! 02-09 New! 02-10 New! 02-11 New! 02-12 New! 02-13

Please before reading proofs, consider reading notes. Note 1 (notation used), Note 2a (about equivalent puzzles) , Note 2b (what is "type"), Note 3 , Note 4 , Note 5 .

New ! Forbidding chains for absolute beginners : the tip that generalizes all known (naked/hidden pairs, Xwing...) and keeps applying when others fail.













Note 1 about notations :
The notation used (suggested by Andrei Zelevinski) is as follows :
Cells: a1, a2, ..., i9 (as in chess).
Rows: R1, R2, ..., R9 (bottom to top).
Columns: Ca, Cb, ..., Ci (left to right).
Blocks: Bb2, Bb5, ..., Bh8 (labeled by central cells).

Abbreviated justification of moves:
e4=7%cell means (the only possibility for e4 is 7).
e4=7%row means (e4 is the only possibility for 7 in its row R4).
e4=7%col means (e4 is the only possibility for 7 in its column Ce).
e4=7%block means (e4 is the only possibility for 7 in its block Be5).

Such moves will be referred as "easy (or simple) eliminations".
A notation tutorial for absolute beginners.

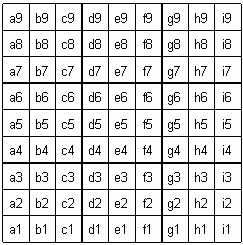
 notation


Note 2a. Some sudokus are equivalent by elementary modifications (e.g. rotating the grid or renumbering). When it's so, I only indicate how to transform one into another, equivalent and already proved. From 2005/05/15 to 2006/01/15, all the (non-obvious) puzzles presented on sudoku.com.au were equivalent to one of this list : 09-12, 09-20, 09-24, 09-28, 09-30,
which proofs are detailed (in fact there sometimes appeared a sixth type, but it solved using only simple fillings and doesn't concern us, who like to work on tough puzzles). For some others, the way to reduce them to an equivalent already known is graphically detailed, for the others, only written indications. Explore first the graphically detailed ones(e.g. 09-26, 09-29, 10-02, 10-03, 10-04, 10-05) then you'll be able to work out the others.
To see how equivalence is used to translate proofs, look10-08.

note : We must really thank Gath for having heard that this recycling of the same puzzles could lead to monotony, and for now having changed his generator to offer us brand new puzzles !

Note 2b. After Jimmy asked for, a little word on classifying puzzles : I use to give them a "type" : a->b, where
a=number of initially filled cells,
b=number of filled cells after all possible simple eliminations have been performed from the start.
Obviously, two equivalent puzzles always have same type, but beware, two puzzles having same type need not be equivalent. However, since I scan sudoku.com.au's puzzles, same type puzzles always happened to be equivalent.
Here are the types of the only 5 models met From 2005/05/15 to 2006/01/15 :
19->28 (first happened 09/12, detailed proof : 09/12)
19->51 (first happened 09/11, detailed proof : 09/30)
21->27 (first happened 09/13, detailed proof : 09/20)
21->26 (first happened 09/17, detailed proof : 09/28)
20->23 (first happened 09/24, detailed proof : 09/24).
When you face a new puzzle, first check its type first, it might be equivalent to one already proved.

Note 3 Some proofs are not simple. Anyone with any simpler solution is most welcome...

Note 4 Please forgive the author for his bad-webbish-learnt english. I will thankfully appreciate every remark in order to improve the grammary/vocabulary correctness of these pages. (Thanks to Gath and Ken Austin for already helping me once).

Note 5 Thanks for visiting me, please come back soon. You also may email me at brunogreconospam@free.fr (remove "nospam" before using).

Antitroll . 05/11/2005 : Hi all from sudoku.com.au, allow me a last self-contradictory post. It's now 2 days that my nickname is quoted far more than my modesty can afford on comments (self-contradiction : this comment is once more about me...but it's the last one as for me).
1) Please remember that my english is very poor, with 2 consequences :
a) I love non-sudoku comments, they often make me lol (the KQRP soap is a must!), but I'm in fear of entering in such discussions by lack of vocabulary (by the way thanks HH for mentioning Liam's pic : I was quite moved).
b) I'm talking only technical : for sure, my 50 or 100 english words are far enough for talking sudoku !
2) Some people on Internet have a passion : make forums talk about them ( it's called trolling), I definitely don't ! So pro-gbs, please answer no more to antis, and anti-gbs, practice the best strategy against trolling : ignore me !
3) antis : please have a look at former boards, you'll see that apart from each day's puzzle presentation, that I very well can stop, most of my posts are replys to questions from users. Please also have a look at
http://sudoku.com/forums/, you'll see what are technical forums!
4) pros : once more, though I most appreciate your reactions, please do no more answer to antis, in fact I agree with them when they make me realize that I'm invading the board with my comments !
5) pros and cons : anything more on the subject? use this Guestbook. Go to sudoku.com.au
Go to top page
Last modified 08/10/2005.

























l