Just below I give a proof for today's (=10/08) puzzle (big thanks to Paige who corrected 3 (three!!!) typing flaws). If you're interested in equivalent puzzles, go there to see how this proof has been automatically derived from 09/12's proof, after that 09/12's and today's puzzle have been proved equivalent.

Proof of today's :

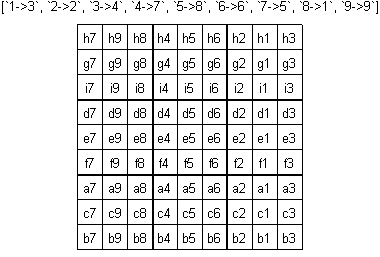
1) Easy eliminations : a2=1%row, i8=7%row, e2=2%row, h2=5%row, g2=7%row, h6=7%block, i2=9%row, e8=4%cell, a8=2%cell, lead to 28 cells filled.

(For easy following of explanations below, complete first the online board with remaining possibilities in each empty cell)

2) Look at 9 in Bh5 : 9 is in Cg, so no other 9's in Cg. 36 are the only choices in h1 and in h3, so you can eliminate all 3s and 6s except these as possibilities in Ch and Blockh2.
Perform the same with the only choices : 19 in b8 and c8, then 46 in b7 and b9, then 12 in b5 and h5. Now we have

3) Look at 8 in Be8. Whether it is in Cd (in which case d5=3%cell), or it is in e9 (in which case c9=3%cell) : c5=4%cell. Follow now easy eliminations (f6=4%block, f5=6%cell, e1=6%block, h3=6%block, h1=3%block, d3=3%block, g5=3%row, d5=8%row, e9=8%block, a7=8%block, c9=3%block, i7=3%block) up to 41 filled cells. Now we have

4) Look at Bb5. Now 21 are in b5c6 no matter the order, eliminate others 2 and 1 from Bb5. Follow then easy eliminations (c4=7%cell, b4=5%cell, e6=5%col, e4=3%block, a6=3%block, a4=6%block) up to 47 filled cells. Now we have :

5) Now look at h5. Whether h5=2 (in which case c6=2%block, c3=8%cell), or h5=1 (in which case i4=8%cell, g1=8%col) : c1=9%cell. Now easy eliminations lead to unique solution.

(Details if needed : c8=1%cell, b8=9%cell, c6=2%cell, b5=1%cell, h5=2%cell, h7=9%cell, c3=8%cell, i3=4%cell, a3=5%cell, f3=7%cell, f7=2%cell, d7=7%cell, b3=2%cell, g1=8%cell, g4=9%cell, g6=6%cell, g7=4%cell, b7=6%cell, i6=1%cell, d6=9%cell, i4=8%cell, f4=1%cell, d4=2%cell, f1=5%cell, d1=1%cell, h9=1%col, i9=6%cell, g9=2%cell, f9=9%cell, d9=5%cell, b9=4%cell, a1=4%col, b1=7%cell).

Note : Equivalent puzzles are : 09/12, 09/26, 09/27, 09/29, 10/02.

back to sandbox

Proof of today's derived from proof of 09/12's puzzle :

Here we are going to explain how to translate 09/12's proof in today's proof. Central diagram below indicate how to :

Exercises : 1) How does data e3=7 of 09/12 translate in today's puzzle ? 2) Where has Column Ca of 09/12 been moved to in today's puzzle? 3) Where has Block Bb5 of 09/12 been moved to in today's puzzle? (Answers)

All right, now ready for proof translation...

Typo tip : In the following, we'll write arguments about today's puzzle in italics in order to distinguish them from 09/12's arguments.

1) First step of 09/12's proof was : "Easy eliminations : c7=8%col, g3=4%col, c5=2%col, c1=7%col, c2=4%col, d1=4%block, c3=9%col, g5=3%cell, g7=2%cell, lead to (for better reading, only remaining possibilities in still empty cells are written)." Translate : c7--> a2 (see dictionary=above diagram), 8--> 1 , col--> row , so first simple elimination "c7=8%col" in 09/12 becomes "a2=1%row" in today's ! Check this stands by looking only at today's grid. Samely g3-->i8, 4-->7, and "g3=4%col" becomes "i8=7%row". Going the same way, we'll get for today's: " Easy eliminations : a2=1%row, i8=7%row, e2=2%row, h2=5%row, g2=7%row, h6=7%block, i2=9%row, e8=4%cell, a8=2%cell, lead to (for better reading, only remaining possibilities in still empty cells are written). "

2) 09/12's proof then said :

"Look at 9 in Be2 : 9 is in R2, so no other 9's in R2.

16 are the only choices in a1 and in b1, so you can eliminate all 1s and 6s except these as possibilities in Row1 and Blockb2.
Perform the same with the only choices : 89 in g8 and g9, then 36 in h9 and i9, then 28 in e1 and e9. We're at"

Apply dictionary (9-->9, Be2-->Bh5,R2-->Cg, and so on), you get for today's

" Look at 9 in Bh5 : 9 is in Cg, so no other 9's in Cg.

36 are the only choices in h1 and in h3, so you can eliminate all 3s and 6s except these as possibilities in Ch and Blockh2.
Perform the same with the only choices : 19 in b8 and c8, then 46 in b7 and b9, then 12 in b5 and h5. We're at "

3) 09/12's proof then said : "Look at 5 in Bh5. Wether it is in R4, in which e4=1%cell, or it is in g5 in which g8=1%cell : e8=3%cell. Follow now easy eliminations (d6=3%block, e6=6%cell, b5=6%block, a1=6%block, b1=1%block, a4=1%block, e2=1%col, e4=5%col, h5=5%block, i7=5%block, h8=1%block, i3=1%block) up to :" Apply dictionary (5-->8, Bh5-->Be8, R4-->Cd, e4-->d5, 1-->3, g5->e8, g8-->c8, e8-->c5, 3-->4 and so on), you get : "Look at 8 in Be8. Whether it is in Cd (in which case d5=3%cell), or it is in e9 (in which case c9=3%cell) : c5=4%cell. Follow now easy eliminations (f6=4%block, f5=6%cell, e1=6%block, h3=6%block, h1=3%block, d3=3%block, g5=3%row, d5=8%row, e9=8%block, a7=8%block, c9=3%block, i7=3%block) up to 41 filled cells and :"

4) 09/12's proof then said :

"Look at Be8. Now 28 are in d8e9 no matter the order, eliminate others 2 and 8 from Be8. Follow then easy eliminations (f8=4%cell, f9=7%cell, d5=7%row, f5=1%block, d7=1%block, f7=6%block) up to :"

Apply dictionary (Be8-->Ba5, 28-->21, d8e9-->b5c6, f8=4-->c4=7 and so on, you get :

"Look at Ba5. Now 21 are in b5c6 no matter the order, eliminate others 2 and 1 from Ba5. Follow then easy eliminations (c4=7%cell, b4=5%cell, e6=5%col, e4=3%block, a6=3%block, a4=6%block) up to :"

5) 09/12's proof then said :

"Now look at e1. Whether e1=2, in which d8=2%block, a8=5%cell, or e1=8, in which f3=5%cell,b2=5%row : b8=9%cell. Now easy eliminations lead to unique solution. "

Apply dictionary : e1-->h5, 2-->2, d8-->c6, a8-->c3, 5-->8, 8-->1, f3-->i4, b2-->g1, b8-->c1, 9-->9, you get :

"Now look at h5. Whether h5=2, in which c6=2%block, c3=8%cell, or g5=1, in which i4=8%cell, g1=8%col : c1=9%cell. Now easy eliminations lead to unique solution."

Hope that now you understand equivalent puzzles a bit more than before...

back to sandbox

Answer of exercises : 1) e3 has been replaced in i5 , 7 has been renamed in 5 , giving i5=5 in today's. 2) Column Ca of 09/12 has been moved to Row R3 of today's. 3) Bb5 moved to Be2. Back to proof